The Measurement of Tissue Optical Properties

The measurement of optical properties i.e. absorption coefficient (μ_a), scattering coefficient (μ_s), and scattering anisotropy (g) of biological tissues is a key challenge in the field of biomedical optics. Information about these parameters is essential in both therapeutic and diagnostic applications of light in medicine. Case in point, optical properties are needed to predict fluence distributions for irradiation procedures such as photodynamic therapy, photocoagulation, and tissue ablation.

Additional, optical properties have a great effect on in vivo diagnostics such as fluorescence spectroscopy and optical imaging, the optical properties themselves can potentially be used to provide metabolic information and diagnose diseases.

So far, a number of techniques have been developed to measure tissue optical properties. The collimated transmission method can be used to measure the total interaction coefficient (μ_a + μ_s). In this technique, a collimated light beam illuminates a thin piece of tissue. Un-scattered transmitted light is detected, while the scattered light is rejected by use of a small aperture. The un-scattered transmitted light can be calculated based on the Beer-Lambert law. The Beer-Lambert law for absorbing and scattering media is l(z) = I₀exp[-(μ_a + μ_s)z], where l(z) is the un-scattered transmitted light intensity after penetrating a depth of z. I₀ is the incident light intensity. I₀, l(z), and z are measured. Therefore, μ_a + μ_s can be determined.

One of the techniques that were previously developed for experimentally measuring absorption and scatter is the integrating sphere measurement method. In this method, a thin slice of tissue is sandwiched between two integrating spheres (spheres) with an entrance and exit port whose inner surface is coated with a diffuse reflecting material. A collimated beam is incident upon the tissue sample. Both the diffuse reflectance and transmittance are measured by integrating the diffusely reflected and transmitted light, respectively. These two measurements are used to determine the absorption coefficient (μ_a) and the reduced scattering coefficient (μ_s) with a model. The model could be based on the adding-doubling method, the Monte Carlo method, delta-Eddington method, or any other light transport theories.

Alternatively, we have a normal incidence video reflectometry technique. In this case, a collimated light beam is normally incident upon a tissue. The spatial distribution of diffuse reflectance is collected using either a CCD camera or an optical fiber bundle. Diffusion theory is used to fit the measured spatial distribution of diffuse reflectance to deduce the optical properties. The measured spatial distribution of diffuse reflectance must be in absolute units unless total diffuse reflectance is measured along with the diffuse reflectance profile. Calibration to absolute units is a sensitive procedure; therefore, this technique is not ideal for a clinical setting.

We can use time-resolved or frequency-domain techniques to measure optical properties, however, these techniques require instrumentation that may not be cost effective for non-research applications. A favorable approach for in vivo optical property measurements is fiber-optic based oblique incidence reflectometry. It is a relatively accurate method for measuring the absorption and reduced scattering coefficients, μ_a + μ_s. Obliquely incident light produces a spatial distribution of diffuse reflectance that is not centered about the point of light incidence. The amount of shift in the center of diffuse reflectance is directly related to the medium’s diffusion length, D. A fiber optic probe may be used to deliver light obliquely and sample the relative profile of diffuse reflectance. Measurement in absolute units is not required. From the profile, it is possible to measure D, perform a curve fit for the effective attenuation coefficient, μ_eff and then calculate μ_a and μ_s.

μ_eff is defined as:                 

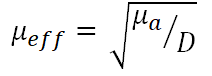
Also read: The Operation of Fiber-optic Based Blood Gas Sensors